Particle Insertion Hydration

Software Technical Information

This is the core module for the particle insertion suite of codes

Languages
C, Python 2.7, LAMMPS Scripting language
Licence
MIT -however, note that LAMMPS is GPL so when used together GPL applies
Documentation Tool
All source code should be documented so please indicate what tool has been used for documentation. We can help you with Doxygen and ReST but if you use other tools it might be harder for us to help if there are problems.
Application Documentation

See PIhydration README file

Relevant Training Material Add a link to any relevant training material.

Purpose of the Module

This software module computes the change in free energy associated with the insertion or deletion of water in dilute or dense conditions in a variety of Thermodynamic Ensembles, where statistical sampling through molecular dynamics is performed under LAMMPS but will be extended to other molecular dynamics engines at a later date. It builds on the PI Core module of codes by adding electrostatic, bond, and angle 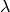\lambda dependent interactions including SHAKE to the Lennard-Jones interactions that were dealt with in PIcore. It differs from the main community approach used to date to compute such changes as it does not use soft-core potentials. Its key advantages over soft-core potentials are: (a) electrostatic interactions can in principle be performed simultaneously with particle insertion (this and other functionalities will be added in a new module); and, (b) essentially exact long-range dispersive interactions using dispersion Particle Mesh Ewald (PMME) or EWALD if desired can be selected at runtime by the user.

Background Information

Particle insertion can be used to compute the free energy associated with hydration/drying, the insertion of cavities in fluids/crystals, changes in salt levels, changes in solvent mixtures, and alchemical changes such as the mutation of amino-acids. in crystals. It can also be used to compute the free energy of solvent mixtures and the addition of salts, which is used in the purification processing industrially, for instance in the purification of pharmaceutical active ingredients. Particle insertion can in principle also be used to compute the free energy associated with changes in the pH, that is the proton transfer from a titratable site to the bulk, for example in water.

Our approach consists of rescaling electrostatic charges of inserted atoms so that they converge to zero faster than inerted Van der Waals atoms where the later uses the geometric mean for Lennard Jones diameters and binding energies, and that bond, angle, and dihedral spring constants and where necessary also bond lengths scale to zero in the same fashion

the effective size of inserted atoms through a parameter 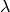\lambda so that all interactions between inserted atoms and interactions between inserted atoms and atoms already present in the system are zero when 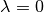\lambda = 0, creating at most an integrable singularity which we can safely handle. In the context of Lennard-Jones type pair potentials, our approach at a mathematical level is similar to Simonson, who investigated the mathematical conditions required to avoid the singularity of insertion. It turns out that a non-linear dependence of the interaction on :math: ‘\lambda’ between inserted atoms and those already present is required (i.e. a simple linear dependence on :math: ‘\lambda’ necessarily introduces a singularity).

The applications of this module use in upcoming modules include computing the free energy changes associated with:

(a) hydration and drying;
(b) the addition of multiple molecules into a condenses environment;
(c) residue mutation and alchemy;
(d) constant pH simulations, this also will also exploit modules created in E-CAM work package 3
    (quantum dynamics); and,
(e) free energy changes in chemical potentials associated with changes in solvent mixtures.

General Formulation

Consider a system consisting of 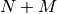N+M degrees of freedom and the Hamiltonian

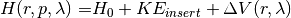
H(r,p,\lambda) =&H_0 + KE_{insert} + \Delta V(r, \lambda)

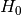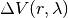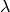where H_0 corresponds to an unperturbed Hamiltonian, and the perturbation \Delta V(r, \lambda) depends nonlinearly on a control parameter \lambda. The first set of N degrees of freedom is denoted by A and the second set of M degrees of freedom is denoted by B. To explore equilibrium properties of the system, thermostats, and barostats are used to sample either the NVT (canonical) ensemble or the NPT (Gibbs) ensemble. 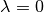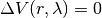The perturbation is devised so that when \lambda = 0, \Delta V(r, \lambda) = 0, B is in purely virtual. When 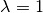\lambda = 1, B corresponds to a fully physical augmentation of the original system.

In the present software module, we include in the perturbation interaction Lennard Jones potenetials, harmonic bond and angle interactions, and electostatic interactions:

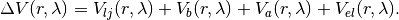
\Delta V(r,\lambda) = V_{lj}(r,\lambda) + V_{b}(r,\lambda) + V_{a}(r,\lambda) + V_{el}(r,\lambda).

where for each inserted atom i

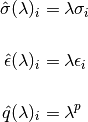
\hat{\sigma}( \lambda)_i &= \lambda \sigma_i \\ \hat{\epsilon}( \lambda)_i &= \lambda \epsilon_i \\ \hat{q}( \lambda)_i &= \lambda ^p \\

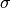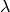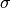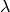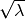and the mixing rule for Van der Waals diameters and binding energy between different atoms uses the geometric mean for atoms pairs where one or more of the atoms is inserted but retains the mixing rule for atoms already present. The dependence of \sigma on \lambda has the consequence that the mean \sigma between a pair of inserted atoms scales as \lambda, but scales as \sqrt{\lambda} when one atom in the pair is inserted and the other is already present. 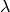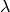The dependence of math:epsilon on \lambda ensures that forces behave regularly when \lambda is very small. These choices of perturbations guarantees that the particle insertion and deletion catastrophes are avoided. Regarding electrostatic interactions, the exponent p allows the rate of convergence electrostatic interactions to zero to be faster than the rate at which that the effective diameters between corresponding Lennard Jones atoms go to zero, so as to ensure divergences are avoided. Currently p = 1.5. 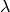The spring constants for harmonic, angular and torsional interactions involving inserted atoms are currently simply multiplied by \lambda.It is also possible to replace bond, angle and torsional interactions involving only inserted atoms with shake constraints. In such cases, the shake constraints are continuously on. For cases where arithmetic sum rules apply to the original system, an additional lambda bases perturbation stage can be applied to transform geometric mean based mixing rules for Lennard Jones interactions to arithmetic mean rules governing interactions between inserted atoms or inserted atoms and original atoms.

Algorithms

At the core of the PI core module there are four functions/codes. The first written in python generates the interpolation points which are the zero’s of suitably transformed Chebyshev functions.

The second code written ln LAMMPS scripting language performs the simulation in user-defined ensembles at the selected interpolation values of :math:’lambda’, at a user-specified frequency, computing two-point central difference estimates of derivatives of the potential energy needed for thermodynamic integration, computing the energy functions for all values of :math:’lambda’ in the context of MBAR. The user also specifies the locations of the inserted particles. The user also specifies whether Particle Mesh Ewald or EWALD should be used for dispersive interactions.

The third code written in python takes the output data from LAMMPPS, prepares it so that free energy differences in the selected ensemble can be computed using MBAR provided by the pymbar suite of python codes of the Chodera group.

The fourth code, also written in python take the LAMMPS output and performs the thermodynamic integration.

Source Code

All files can be found in the PIhydration subdirectory of the particle_insertion git repository.

Scaling and Performance

As the module uses LAMMPS, the performance and scaling of this module should essentially be the same, provided data for thermodynamic integration and MBAR is not generated too often. In the case of thermodynamic integration, this is due to the central difference approximation of derivatives, and in the case of MBAR, it is due to the fact that many virtual moves are made which can be extremely costly if the number of interpolating points is large. Also, when using PMME, the initial setup cost is computationally expensive, and should, therefore, be done as infrequently as possible. A future module in preparation will circumvent the use of central difference approximations of derivatives.