Test case: a dimer solvent¶
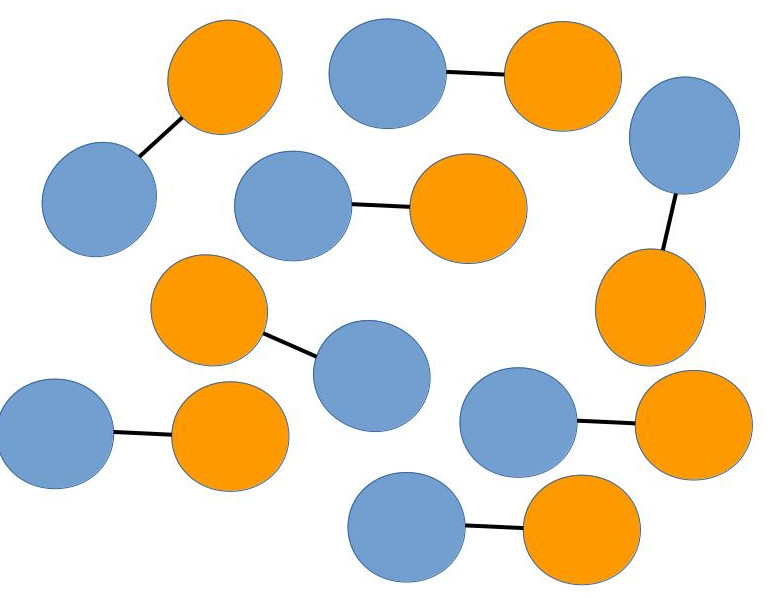
Here we describe a physical system in which the software modules dealing with
charge dipole moments in DPD simulations can be tested.
It is a polarizable fluid made of harmonically bonded dimers
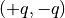 , pictorially represented on the left (not in scale).
Fixing appropriately the partial charge
, pictorially represented on the left (not in scale).
Fixing appropriately the partial charge  and the Bjerrum length
and the Bjerrum length 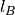 , this system mimics water in an oil
background, as long as the dielectric properties are concerned.
, this system mimics water in an oil
background, as long as the dielectric properties are concerned.
We recall that the electric permittivity is 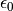 for vacuum, and
for vacuum, and
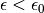 for a medium. The medium effect can be split into
a background and a relative term
for a medium. The medium effect can be split into
a background and a relative term 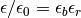 .
The background is constant and uniform, whereas the explicit term is due to
dynamic microscopic objects (dimers in this case) which carry a charge dipole
moment. The strength of electrostatic interactions in a background is set by the bare Bjerrum length
.
The background is constant and uniform, whereas the explicit term is due to
dynamic microscopic objects (dimers in this case) which carry a charge dipole
moment. The strength of electrostatic interactions in a background is set by the bare Bjerrum length 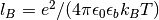 . On the other hand, from linear response theory, the bulk value of the relative permittivity is
. On the other hand, from linear response theory, the bulk value of the relative permittivity is
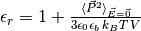 ,
where tin-foil boundary conditions are assumed.
,
where tin-foil boundary conditions are assumed.
Two types of beads are present in the simulation, solp and solm, the solvent positive
and negative partial charges, respectively. We fix the bare Bjerrum length
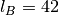 (appropriate for oil [1]), the repulsion parameter
(appropriate for oil [1]), the repulsion parameter 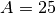 , the harmonic spring
constant
, the harmonic spring
constant 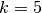 , the bead density
, the bead density 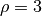 , the partial charges
, the partial charges 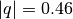 and the Gaussian
smearing length
and the Gaussian
smearing length 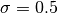 . All quantities are given in DPD units,
where
. All quantities are given in DPD units,
where 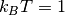 ,
, 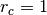 and
and 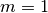 .
This fluid has a relative permittivity
.
This fluid has a relative permittivity 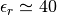 , as can be checked
using the
, as can be checked
using the gen_dipole.f90 utility. This value is compatible with the ratio
of water and oil permittivities 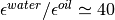 .
.
The FIELD file defining the composition and interactions for a system of
volume 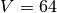 is
is
DL_MESO charged harmonic dimers with dpd repulsion
SPECIES 2
solp 1.0 0.46 0
solm 1.0 -0.46 0
MOLECULES 1
DIMER
nummols 96
beads 2
solp 0.0 0.0 0.0
solm 0.1 0.0 0.0
bonds 1
harm 1 2 5.0 0.0
finish
INTERACTIONS 3
solp solp dpd 25.0 1.0 4.5
solm solm dpd 25.0 1.0 4.5
solp solm dpd 25.0 1.0 4.5
CLOSE
| [1] | Notice that the physical length scale is set choosing 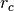 : if we choose : if we choose 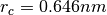 (appropriate to match water density at room temperature if
(appropriate to match water density at room temperature if 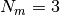 , i.e., one bead represents
three water molecules), the Bjerrum length of oil in DPD units is , i.e., one bead represents
three water molecules), the Bjerrum length of oil in DPD units is 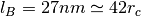 ,
hence the value given above for the oil background. ,
hence the value given above for the oil background. |