The information in this section describes ESPResSo++ as a whole. Information specific to the additions in this module are in subsequent sections.

Name: Coarse-graining procedure for one component melts
Language: Python (2.7) and C++
Licence: GPL <https://opensource.org/licenses/gpl-license>
Documentation Tool: Sphinx and Doxygen
Application Documentation: http://espressopp.github.io/
Relevant Training Material: https://github.com/espressopp/espressopp/tree/master/examples

Coarse-Graining: A Component of the Hierarchical Equilibration Strategy for Polymer Melts¶

Purpose of Module
Background Information
Building and Testing
Source Code
References

The module is an implementation of the existing hierarchical strategy [1] for the equilibration of simple one-component polymer melts in ESPResSO++.

Purpose of Module ¶

To study the properties of polymer melts by numerical simulations, equilibrated configurations must be prepared. However, the relaxation time for high molecular weight polymer melts is huge and increases, according to reptation theory, with the third power of the molecular weight. Hence, an effective method for decreasing the equilibration time is required. The hierarchical strategy pioneered in Ref. [1] is a particularly suitable way to do this. The present module provides a part of that method described below.

To decrease the relaxation time, microscopic monomers are coarse-grained (CG) by mapping each subchain with 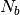$N_{b}$ monomers onto a soft blob. The CG system is then characterized by a much lower molecular weight and thus is equilibrated quickly. The present module provides a python script which performs this coarse-graining procedure. The implementation detail is in following below.

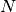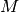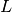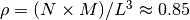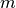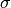The microscopic configuration of $N$ polymers consisted of $M$ monomers is prepared. The system size $L$ is determined by the number of density $\rho= (N \times M) /L^3 \approx 0.85$ . $m$ and $\sigma$ stands for the mass and the diameter of monomers.
The configuration of 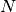$N$ CG chain at 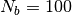$N_{b}=100$ is generated from the microscopic configuration.

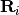The position of $i$ -th softblobs $\mathbf{R}_{i}$ is determined by 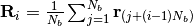$\mathbf{R}_{i} = \frac{1}{N_{b}}\sum^{N_{b}}_{j=1} \mathbf{r}_{(j + (i-1)N_{b})}$ , where 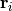$\mathbf{r}_{i}$ stands for the position of $i$ -th monomers.

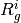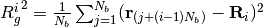The radius of gyration $i$ th softblobs $R_{g}^i$ is also determined by ${R_{g}^i}^2 = \frac{1}{N_{b}}\sum^{N_{b}}_{j=1} (\mathbf{r}_{(j + (i-1)N_{b})} - \mathbf{R}_{i})^2$ .
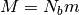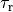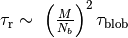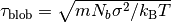The CG configuration is equilibrated by NVT MD simulation with mass of softblobs $M = N_{b}m$ during the equilibration time $\tau_{\rm{r}}$ defined as $\tau_{\rm{r}} \sim\ \left( \frac{M}{N_{b}}\right)^2 \tau_{\rm{blob}}$ , where $\tau_{\rm{blob}}=\sqrt{m N_{b}\sigma^2/k_{\rm{B}}T}$ .

Hence, CPU time 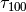$\tau_{100}$ for softblobs with 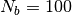$N_{b}=100$ is estimated as $\tau_{100} \sim\ N \times \left( \frac{M}{N_{b}}\right)^3 \tau_{\rm{blob}}$ .
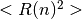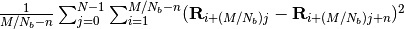After equilibrating a configuration, we continue to carry out MD simulation for adopting the snapshot which show ideal mean square internal distance (MSID) $<R(n)^2>$ represented as $\frac{1}{M/N_{b} -n}\sum^{N-1}_{j=0}\sum^{M/N_{b} -n}_{i=1}(\mathbf{R}_{i+(M/N_{b})j} - \mathbf{R}_{i+(M/N_{b})j+n})^2$ .

Ideal MSID means the MSID of CG chains generated from fully equilibrated microscopic configurations.

A snapshot is captured in each $\tau_{\rm{blob}}$ .