Hierarchical Strategy for Simple One-Component Polymer Melts: constrain-com¶

Purpose of Module
Background Information
Testing
Source Code
References

Reference [1] describes the principles of a hierarchical strategy to equilibrate simple one-component polymer melts described in terms of atomistic or coarse-grained (bead-spring) models. The present module is part of our implementation of this method in ESPResSO++.

Purpose of Module ¶

To study the properties of polymer melts by numerical simulations, equilibrated configurations must be prepared. However, the relaxation time for high molecular weight polymer melts is huge and increases, according to reptation theory, with the third power of the molecular weight. Hence, an effective method for decreasing the equilibration time is required. The hierarchical strategy pioneered in Ref. [1] is a particularly suitable way to do this. The present module is part of a suite of programs which realize this method within the framework of the simulation package ESPResSO++.

To decrease the relaxation time, microscopic monomers are coarse-grained (CG) by mapping each subchain with 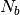$N_{b}$ monomers onto a soft blob. The CG system is then characterized by a much lower molecular weight and thus is equilibrated quickly. One thus obtains a configuration that is equilibrated on large scales but does not provide information about the structure on smaller (i.e. more fine-grained (FG)) scales.

To obtain the latter, the resolution is step-by-step increased by recursively applying a fine-graining procedure to the previous (more coarse-grained) level. In such a fine-graining step, each CG polymer chain is replaced with a more fine-grained chain, by dividing a CG blob into several FG blobs. In the last step, microscopic monomers are reinserted into CG blobs.

The resulting set of FG blobs is set up in such a way that its conformation is consistent with the conformation at the more coarse-grained level. After this setup, the local FG conformation is relaxed into a local equilibrium, again consistent with the (fixed) CG blobs. Consistency here means that the center of mass (COM) of the set of FG blobs coincides with the center of the corresponding CG blob, during an initial period which is long enough that nearly perfect local equlibrium is reached. After that, the constraint is lifted.

The present module provides the C++ class for applying a suitable constraint that conserves the position of the COM of N FG blobs.