Hierarchical Strategy for Simple One-Component Polymer Melts: md-softblob¶
Reference [1] describes the principles of a hierarchical strategy to equilibrate simple one-component polymer melts described in terms of atomistic or coarse-grained (bead-spring) models. The present module is the central part of our implementation of this method in ESPResSO++.
Purpose of Module¶
To study the properties of polymer melts by numerical simulations, equilibrated configurations must be prepared. However, the relaxation time for high molecular weight polymer melts is huge and increases, according to reptation theory, with the third power of the molecular weight. Hence, an effective method for decreasing the equilibration time is required. The hierarchical strategy pioneered in Ref. [1] is a particularly suitable way to do this. The present module is the central part that controls a suite of programs which realize this method within the framework of the simulation package ESPResSO++.
To decrease the relaxation time, microscopic monomers are
coarse-grained (CG) by mapping each subchain with 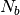 monomers
onto a soft blob. The CG system is then characterized by a much
lower molecular weight and thus is equilibrated quickly. One thus
obtains a configuration that is equilibrated on large scales
but does not provide information about the structure on smaller
(i.e. more fine-grained (FG)) scales.
monomers
onto a soft blob. The CG system is then characterized by a much
lower molecular weight and thus is equilibrated quickly. One thus
obtains a configuration that is equilibrated on large scales
but does not provide information about the structure on smaller
(i.e. more fine-grained (FG)) scales.
To obtain the latter, the resolution is step-by-step increased by recursively applying a fine-graining procedure to the previous (more coarse-grained) level. In such a fine-graining step, each CG polymer chain is replaced with a more fine-grained chain, by dividing a CG blob into several FG blobs. In the last step, microscopic monomers are reinserted into their CG blobs.
The resulting set of FG blobs is set up in such a way that its conformation is consistent with the conformation at the more coarse-grained level. After this setup, the local FG conformation is relaxed into a local equilibrium, again consistent with the (fixed) CG blobs.
The present module implements the actual coarse-graining step, which is therefore described in more detail:
A polymer chain, originally consisting of 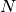 monomers, is replaced by a coarse-grained (CG) chain consisting of
monomers, is replaced by a coarse-grained (CG) chain consisting of
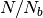 soft blobs linked by a harmonic bond potential,
soft blobs linked by a harmonic bond potential,
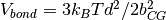 , and an angular bond-bending
potential
, and an angular bond-bending
potential 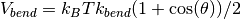 . Here
. Here
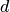 is the distance and
is the distance and 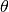 is the angle between
consecutive bonds. The interactions between non-bonded soft blobs are
taken into account by a repulsive pair potential
is the angle between
consecutive bonds. The interactions between non-bonded soft blobs are
taken into account by a repulsive pair potential 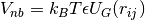 . Here
. Here 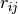 is the center-to-center
distance between the two blobs,
is the center-to-center
distance between the two blobs, 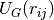 is a Gaussian
function with variance
is a Gaussian
function with variance 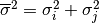 and
and
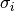 is the gyration radius of blob number
is the gyration radius of blob number
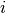 . The gyration radius
. The gyration radius 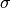 is in turn
fluctuating. This fluctuation is controlled by the potential
is in turn
fluctuating. This fluctuation is controlled by the potential
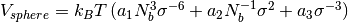 .
Equilibrated configurations of soft blobs are generated by
Molecular Dynamics (MD) simulations based on the above model.
.
Equilibrated configurations of soft blobs are generated by
Molecular Dynamics (MD) simulations based on the above model.
Within the module, the following classes have been implemented or modified:
- A
VSpherePairclass for calculating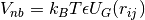
- A
VSphereSelfclass for calculating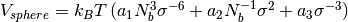
- A
Particleclass for comunicating the property “radius” between different cores - A
LangevinThermostatOnRadiusclass for simulating the fluctuations of the radii of the blobs
Background Information¶
The implementation of this module is based on ESPResSO++. You can learn about ESPResSO++ from the following links:
- ESPResSO++ documentation: http://espressopp.github.io/ESPResSo++.pdf
- ESPResSO++ source code: https://github.com/espressopp/espressopp
Testing¶
Explanation of installation:
After installing this module, it can be tested by a Python script found under the following link:
Source Code¶
This module has been merged into ESPResSo++:
References¶
| [1] | (1, 2) : http://pubs.acs.org/doi/abs/10.1021/mz5000015, preprint available via https://arxiv.org/abs/1610.07511 |