Caesar Anharmonic Calculation Library¶
Purpose of Module¶
The Caesar anharmonic calculation library aims to provide an efficient method for calculating vibrational properties beyond the harmonic approximation; under the vibrational self-consistent harmonic approximation (VSCHA) [Errea_ea1] or using vibrational self-consistent field theory (VSCF) [Christiansen1].
| [Errea_ea1] | (1, 2) Anharmonic free energies and phonon dispersions from the stochastic self-consistent harmomic approximation: Application to platinum and palladium hydrides. https://doi.org/10.1103/PhysRevB.89.064302 |
| [Christiansen1] | Vibrational structure theory: new vibrational wave function methods for calculation of anharmonic vibrational energies and vibrational contributions to molecular properties. https://doi.org/10.1039/B618764A |
Theory¶
Fitting the Potential Energy Surface¶
Caesar models the nuclear potential energy surface (PES) using a truncated Taylor expansion in normal-mode coordinates. Constructing and fitting this model happens over several steps:
- Firstly, a set of symmetry-invariant basis functions are generated, using the crystal symmetries as calculated by spglib.
- Secondly, a set of nuclear coordinates
are generated at which the PES will be sampled.
- Thirdly, electronic structure calculations are performed at each coordinate, using the Caesar electronic structure interface.
- Finally, the results of the electronic structure calculations, including calculated energies, forces and other information, are used to calculate the basis function coefficients.
As with the harmonic calculation, the anharmonic calculation uses the non-diagonal supercell method [Lloyd-Williams_Monserrat1] to reduce the total computational cost of the electronic structure calculations where possible.
| [Lloyd-Williams_Monserrat1] | Lattice dynamics and electron-phonon coupling calculations using nondiagonal supercells. https://doi.org/10.1103/PhysRevB.92.184301 |
The Vibrational Self-Consistent Harmonic Approximation¶
VSCHA approximates the eigenstates of the system as those which diagonalise an
effective harmonic potential  . The effective harmonic
potential
. The effective harmonic
potential  implemented by Caesar has the same
functional form and normal modes
implemented by Caesar has the same
functional form and normal modes 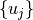 as the harmonic potential
as the harmonic potential
 , but has a different set of frequencies
, but has a different set of frequencies 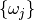 .
.
The frequencies 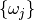 are calculated as those which minimise the free
energy of the anharmonic PES with respect to the VSCHA eigenstates [Errea_ea1].
are calculated as those which minimise the free
energy of the anharmonic PES with respect to the VSCHA eigenstates [Errea_ea1].
Vibrational Self-consistent Field Theory¶
Traditional VSCF separates the PES 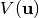 into a sum of single-mode
effective potentials
into a sum of single-mode
effective potentials 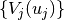 , each of which is the expectation of
, each of which is the expectation of
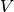 with respect to all modes other than
with respect to all modes other than 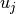 . The Hamiltonian
corresponding to each mode is then constructed in the VSCHA eigenbasis, and this is
diagonalised to give the single-mode VSCF eigenstates
. The Hamiltonian
corresponding to each mode is then constructed in the VSCHA eigenbasis, and this is
diagonalised to give the single-mode VSCF eigenstates 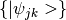 . This
process can be written as two equations,
. This
process can be written as two equations,
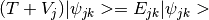
and
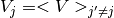
These equations are solved self-consistently, using a Pulay scheme [Pulay].
The VSCF method implemented by Caesar differs from traditional VSCF methods in that rather than separating the PES single-mode potentials, the PES is instead separated into single-subspace potentials, where each subspace contains a complete set of modes whose frequencies are degenerate as a result of symmetry. This implementation of VSCF is symmetry invariant, unlike the single-mode methods.
| [Pulay] | Convergence acceleration of iterative sequences. The case of scf iteration.https://doi.org/10.1016/0009-2614(80)80396-4 |
Performing Calculations¶
Prior to performing anharmonic calculations, a harmonic calculation must be performed. This can be done using the Caesar Harmonic Calculation Library, or the Hessian matrix of the undisplaced structure can be read using the Caesar electronic structure interface.
Like running the Caesar Harmonic Calculation Library, running the Caesar Anharmonic Calculation Library is a four-stage process.
- Firstly,
caesar setup_anharmonicparses the input data and reads the output of the harmonic calculation. It then generates a directory structure containing directories in which all the necessary electronic structure calculations must be run.- Secondly,
caesar run_anharmonicperforms the electronic structure calculations, using the Caesar electronic structure interface. There is no connection between the separate electronic structure calculations, so they can be run sequentially, in parallel, or across multiple computers as desired.- Thirdly,
caesar calculate_potentialuses the results of the electronic structure calculations to fit the anharmonic potential.- Finally,
caesar calculate_anharmonic_observablescalculates the vibrational properties of the crystal under VSCHA and VSCF.
The calculated properties are written to an anharmonic_observables directory. These
can be visualised using the various caesar_plot_ utilities.
As with the harmonic stages, each anharmonic stage has its own helptext, which can be
accessed through the caesar executable by calling caesar --help.
Source Code¶
The source code for Caesar anharmonic library is available from the src/anharmonic
directory of the Caesar repository