FFTXlib¶
Purpose of Module¶
FFTXlib module is a collection of driver routines for complex 3D fast Fourier transform (FFT) libraries to be used within planewave-based electronic structure calculation software.
Generally speaking, FFT algorithm requires a data array to act on, a clear description of the
input-output sequence and transform domains.
In the context of planewave based electronic structure calculations, the data array may hold elements such as
electronic wavefunction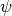 
or charge density 
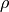or their functions.
The transform domains are direct (real) and reciprocal space,
the discretization in real space is represented as a uniform grid of the unit cell and
the discretization of the reciprocal space is in the basis of planewaves whose wavevectors
are multiples of reciprocal space vectors 
.
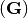To understand the main motivation behind FFTXlib routines we need to clarify the differences between the representation of wavefunction and charge density in planewave based codes:
In these codes, the expansion of wavefunction in planewave basis is
truncated at a cut-off wave-vector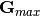 
.
Since density is the norm-square of the wavefunction, the expansion that is consistent with
the one of wavefunctions requires a cut-off wavevector twice that of wavefunctions: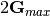 
.
Meanwhile, the real space FFT domain is often only defined by one uniform grid of the unit cell,
so the array sizes of both 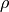and 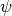in their real space representation are the same.
Therefore, to boost optimization and to reduce numerical noise, the library implements two possible options while performing FFT:
in one ( ‘Wave’) the wavevectors beyond 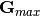are ignored,
in the other ( ‘Rho’ ) no such assumption is made.
Another crucial feature of FFTXlib is that some approximations in the electronic structure calculations
(such as usage of non-normconserving pseudopotentials) require that density is not just
norm-square of wavefunctions, but has spatially localized extra components. In that case,
these localized contributions may require higher G-vector components than the ones needed for density
(
).
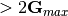Hence, in such systems, the density array in reciprocal space has more elements
than the norm-conserving case (in other words a finer resolution or a denser grid is needed in real space)
while the resolution needed to represent wavefunctions are left unchanged.
To accommodate for these different requirements of grid size, and to be able to make Fourier transforms back and forth between them,
the FFTXlib routines explicitly require descriptor arguments which define the grids to be used. For example,
if potential is obtained from density, the FFT operations on it should use the denser grid;
while FFT on wavefunctions should use the smoother grid (corresponding to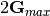 
as defined before).
When the Hamiltonian’s action on wavefunctions are being calculated, the potential should be
brought from dense to smooth grid.
But when the density is being calculated, wavefunction normsquare should be carried from smooth to dense grid.
A final important feature of FFTXlib is the index mapping. In the simple case of no parallelization,
as a choice, the reciprocal space arrays are ordered in increasing order of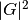 
while the real space arrays are sorted in column major order.
Therefore for FFT to be performed, a map between these two orders must be known.
This index map is created and preserved by the FFTXlib.
In summary, FFTXlib allows the user to perform complex 3D fast Fourier transform (FFT) in the context of plane wave based electronic structure software. It contains routines to initialize the array structures, to calculate the desired grid shapes. It imposes underlying size assumptions and provides correspondence maps for indices between the two transform domains.
Once this data structure is constructed, forward or inverse in-place FFT can be performed. For this purpose FFTXlib can either use a local copy of an earlier version of FFTW (a commonly used open source FFT library), or it can also serve as a wrapper to external FFT libraries via conditional compilition using pre-processor directives. It supports both MPI and OpenMP parallelization technologies.
FFTXlib is currently employed within Quantum Espresso package, a widely used suite of codes for electronic structure calculations and materials modeling in the nanoscale, based on planewave and pseudopotentials. FFTXlib is also interfaced with “miniPWPP” module that solves the Kohn Sham equations in the basis of planewaves and soon to be released as a part of E-CAM Electronic Structure Library.
Background Information¶
FFTXlib is mainly a rewrite and optimization of earlier versions of FFT related routines inside Quantum ESPRESSO pre-v6;
and finally their replacement.
This may shed light on some of the variable name choices, as well as the default of 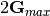cut-off
for the expansion of the smooth part of the charge density, and the required format for lattice parameters in order to build the
FFT domain descriptor.
Despite many similarities, current version of FFTXlib dramatically changes the FFT strategy in the parallel execution,
from 1D+2D FFT performed in QE pre v6
to a 1D+1D+1D one; to allow for greater flexibility in parallelization.
Building and Testing¶
A stable version of the module can be downloaded using this link .. when fftxlib has its own repo, this link can be moved there. Current installation and testing are done with gfortran compiler, version 4.4.7. The configuration uses GNU Autoconf 2.69.
The commands for installation are:
$ ./configure
$ make libfftx
As a result, the library archive “libfftx.a” is produced in src directory, and symbolicly linked to a “lib” directory.
To see how the library works in a realistic case scenario of an electronic structure calculation, run:
$make FFTXexamples
A mini-app will be compiled in src directory and will be symbolicly copied into bin directory.
The mini-app simulates an FFT scenario with a test unit cell, and plane wave expansion cutoff.
It creates the FFT structures and tests forward and backward transform on sample array and reports timings.
Read the README.examples documentation in the examples subdirectory for further details.
Source Code¶
The FFTXlib bundle corresponding to the stable release can be downloaded from this link
The source code itself can be found under the subdirectory src.
The development is ongoing.
The version that corresponds to the one of examples and tests can be obtained with SHA 31a6f4ecbb7ce474b0c87702c716713758f99a0a. This will soon be replaced with a version tag.
Further Information¶
This documentation can be found inside the docs subdirectory.
The FFTXlib is developed with the contributions of C. Cavazzoni, S. de Gironcoli, P. Giannozzi, F. Affinito, P. Bonfa’, Martin Hilgemans, Guido Roma, Pascal Thibaudeau, Stephane Lefranc, Nicolas Lacorne, Filippo Spiga, Nicola Varini, Jason Wood, Emine Kucukbenli.