Software Technical Information

Name
FBTS-MPI
Language
Fortran
Licence
MIT

FBTS_MPI

Purpose of Module

The FBTS-MPI module implements the Forward-Backward Trajectory Solution (FBTS) to the quantum-classical Liouville equation [KapralCiccotti1999] developed by Hsieh and Kapral [HsiehKapral2012], [HsiehKapral2013].

In the case of a many-body system that can be partitioned into a quantum subsystem and classical environment, this module can be used in the calculation of time-dependent observables. The purpose of this module is to provide an efficient and approximate method to study the nonadiabatic dynamics of these systems.

Background Information

In this approximate quantum dynamics method both the quantum subsystem and classical-like environment are transformed into a continuous phase space representation. This is achieved through a partial Wigner transform over the environmental degrees of freedom and a mapping representation for the quantum subsystem, wherein the subsystem degrees of freedom are represented by coherent state variables: 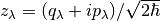z_\lambda = (q_\lambda + ip_\lambda) / \sqrt{2\hbar}.

Classical-like equations of motion are then used to evolve an ensemble of Monte Carlo sampled trajectories through time and the matrix elements of the average value of a time-dependent operator, (having undergone the Wigner transform):

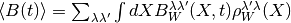
\langle B(t) \rangle = \sum_{\lambda \lambda'} \int dX B_W^{\lambda \lambda'}(X,t) \rho_W^{\lambda' \lambda}(X)

is calculated by the FBTS method using,

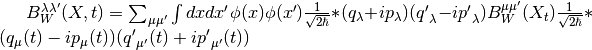
B_W^{\lambda \lambda'}(X,t) = \sum_{\mu \mu'} \int dx dx' \phi(x) \phi(x') \frac{1}{\sqrt{2\hbar}} * (q_\lambda + i p_\lambda)({q'}_\lambda - i {p'}_\lambda) B_W^{\mu \mu'}(X_t) \frac{1}{\sqrt{2\hbar}} * (q_\mu(t) - i p_\mu (t))({q'}_{\mu'}(t) + i {p'}_{\mu'}(t))

where 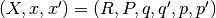(X,x,x') = (R,P,q,q',p,p') and \phi = (2\pi\hbar^{-N}) e^{-\sum(q^2_\nu + p^2_\nu / 2\hbar)}.

Applications

The particular system that this FBTS-MPI module has been built for is in the study of excitation energy transfer in biological light harvesting systems, so-called protein-pigment complexes, through the use of the Frenkel exciton model. [IshizakiFleming2009PNAS] The total Hamiltonian of this system is: 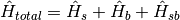\hat{H}_{total} = \hat{H}_{s} + \hat{H}_{b} + \hat{H}_{sb}.

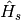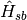In this model the quantum subsystem of interest, \hat{H}_{s}, is the electronic excited states of the pigment molecules, the surrounding vibrational environment, \hat{H}_{b}, is represented as a collection of harmonic oscillatorsand the interaction between the two, \hat{H}_{sb}, is characterized by the spectral density.

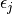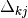Specifically, the subsystem Hamiltonian is built such that the diagonal elements is the site energy, \epsilon_j of a particular pigment, j, with the coupling between the pigments on the diagonals, \Delta_{kj}:

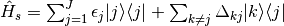
\hat{H}_s = \sum_{j=1}^J \epsilon_j |j \rangle \langle j| + \sum_{k \neq j} \Delta_{kj} |k \rangle \langle j|

The Hamiltonian of the bath is written as, where N is the total number of bath oscillators:

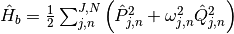
\hat{H}_{b} = \frac{1}{2}\sum_{j,n}^{J,N}\Big( \Hat{P}_{j,n}^2 + \omega_{j,n}^2 \hat{Q}_{j,n}^2\Big)

Lastly, the coupling Hamiltonian:

\hat{H}_{sb} = -\sum_{j,n} c_{j,n} \hat{Q}_{j,n} |j\rangle \langle j|

In this module an approximate form of the spectral density is used, known as the Debye spectral density given below:

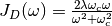
J_D(\omega) = \frac{2\lambda\omega_c\omega}{\omega^2 + \omega_c^2}

The initial application for this module is in examining the mechanisms of exciton transport, which can be studied through the time-dependent exciton site populations for a given light-harvesting complex. The approximate nature of this dynamics method combined with the parallelization of the trajectory ensemble allows one to model exciton transport in large systems with many pigments that would otherwise be prohibitively expensive to simulate.

Building and Testing

In order to compile this module, two files are required, FBTS_MPI.f90 and luxury.f90, one contains the FBTS method and the other returns a random number. Both of these files are located in the ./source sub-directory and can be compiled using:

mpifort FBTS_MPI.f90 luxury.f90 -o FBTS_MPI.x

Upon successful compilation of the code execution of the code requires two input files, one containing relevant information concerning the simulation and the subsystem Hamiltonian matrix in units of wavenumbers.

The file Input_Data.dat contains the simulation parameters and can be easily modified. The number of states of the system, the state in which the initial excitation will occur and the number of trajectories this module will complete can be changed. The influence of the bath can also be adjusted through the parameters that will define the Debye spectral density, the characteristic frequency of the bath, :math:omega_c, the reorganization energy and the number of bath oscillators.

There are three parameters that concern the time length of the simulation, num_timestep, timestep and timestep_block. The total time length of the simulation is determined by: num_timestep * timestep. The parameter timestep_block determines at what interval the time-dependent observables will be calculated and collected.

An example of this Input_Data.dat file and subsystem Hamiltonian matrix can be found in the ./tests/Dimer_Model sub-directory. In order to test the code move the executable to the this sub-directory and compare the output site populations against the exact results from [IshizakiFleming2009] Figure 4(b). Remember that the output provided by the module is given in atomic units of time and must be converted to femtoseconds to compare.

Another model is provided for testing, the light harvesting complex known as the Fenna-Matthews-Olson (FMO) complex that contains 7 states, the exact results are from [WilkinsDattani2015].

The output from the FBTS_MPI module should be in good agreement to the exact results.

Source Code

The FBTS_MPI module source code is located at: FBTS_MPI.

References

[KapralCiccotti1999]
  1. Kapral, G. Ciccotti, J. Chem. Phys. 110 (1999) 8919 DOI: 10.1063/1.478811
[HsiehKapral2012]
  1. Hsieh, K. Raymond, J. Chem. Phys. 137 (2012) 22A507 DOI: 10.1063/1.4736841
[HsiehKapral2013]
  1. Hsieh, K. Raymond, J. Chem. Phys. 138 (2013) 134110 DOI: 10.1063/1.4798221
[IshizakiFleming2009]
  1. Ishizaki, G. R. Fleming, J. Chem. Phys. 130 (2009) 234111 DOI: 10.1063/1.3155372
[IshizakiFleming2009PNAS]
  1. Ishizaki, G. R. Fleming, PNAS 106 (2009) 17255 DOI: 10.1073/pnas.0908989106
[WilkinsDattani2015]
  1. Wilkins, N. Dattani, J. Chem. Theory Comput. (2015) 3411 DOI: 10.1021/ct501066k