Trotter Based Quantum Classical Surface Hopping Propagator - Single Path¶
Abstract¶
The present module is a highly refactored version of a code based on a highly cited algorithm published by D. Mackernan, G.Ciccotti and R. Kapral [Mackernan]. The module software has been entirely refactored in modern C++ (GNU 2011 or higher) so as to: (a) run with high-efficiency on massively parallel platforms under OpenMP or MPI; and (b) be at the core of additional software modules aimed at addressing important issues such as improving the speed of convergence of estimates using correlated sampling, and much more realistic treatment of the classical bath, and connecting to other problems such as constant pH simulation through an effective Hamiltonian.
Purpose of Module¶
Quantum rate processes in condensed phase systems are often computed by combining quantum and classical descriptions of the dynamics including non-adiabatic coupling, using propagators which amount to quantum path integrals in a partial Wigner phase space representation, such as the mixed quantum-classical Dyson equation and variants thereof, or the Trotter decomposition of the quantum-classical propagator.
Background Information¶
An understanding of the dynamical properties of condensed phase quantum systems underlie the description of a variety of quantum phenomena in chemical and biological systems. The development of schemes for the efficient and accurate simulation of the quantum dynamics of such systems is an an active area of research in chemical physics, and is essential if problems of chemical interest involving complex molecular species in the condensed phase are considered.
In investigations of the dynamical properties of quantum
statistical mechanical systems, one is often interested in the
average value of some operator when the system evolves from a
given initially prepared distribution described by the density
matrix 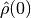 . In such cases the quantum mechanical
average value of an operator
. In such cases the quantum mechanical
average value of an operator 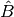 is given by
is given by
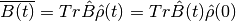 . Here,
. Here,
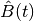 evolves in time through the Heisenberg equation of motion.
In many applications, it is useful to partition the system into a subsystem and
a bath. A phase space description of the bath can be obtained by
taking a partial Wigner transform over the bath coordinate
evolves in time through the Heisenberg equation of motion.
In many applications, it is useful to partition the system into a subsystem and
a bath. A phase space description of the bath can be obtained by
taking a partial Wigner transform over the bath coordinate 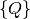 representation
of the full quantum system. In this partial Wigner representation the expectation value of
representation
of the full quantum system. In this partial Wigner representation the expectation value of 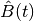 takes the
takes the
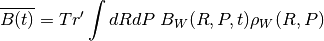
where the prime on the trace indicates a trace over the subsystem degrees of freedom.
The software module developed here is based on a Trotter-based scheme for simulating quantum-classical Liouville dynamics in terms of an ensemble of surface-hopping trajectories. The method can be used to compute the dynamics for longer times with fewer trajectories than the sequential short-time propagation (SSTP) algorithm, which is also based on surface-hopping trajectories. The full derivation of the algorithm is given in [Mackernan]. Here the software focus is to refactor the original code which until now was a purely serial so that it can be used efficiently on massively parallel machines. For mathematical details, we refer the reader to eq.30-35 of the paper.
Applications¶
The applications of quantum surface hopping include, among others, non-adiabatic chemical rate processes involving electronic, vibrational or other degrees of freedom, decoherence in open quantum systems and quantum transport processes. Decoherence due to coupling with the environment is a fundamental difficulty in the development of quantum computing. The ability to predict, control and reduce decoherence requires an adequate description of the associated non-adiabatic processes taking place. Quantum effects and frequently non-adiabaticity also underlie the study of ultra-fast rate processes in solution.
Algorithms and Software Implementation¶
The current Single Path code has three main advantages over the original version. First it is separated into files based on function for better readability. For example the ‘transition_matrix.cpp’ file is where the transition matrix and associated functions are defined, etc. Secondly input parameters are read from an Input file, so the code no longer needs to be recompiled to adjust these parameters. And finally the code has been altered to run in parallel which allows for a significant reduction in runtime.
Compiling¶
All current versions of this code use the GNU scientific library version 2.5 for random number generation.
OpenMP version:
With the GNU compiler, gcc version 6.3.0 or greater is required.
On the Kay cluster this can be done as follows:
module load gcc/8.2.0
module load gsl/gcc/2.5
Compile command;
g++ -o run main.cpp bath_setup.cpp density.cpp propagation.cpp transition_matrix.cpp opt_parser.cpp -lgsl -lgslcblas -lm -fopenmp -std=c++11
Run command:
export OMP_NUM_THREADS=[number of OpenMP threads]; ./run Input
With the Intel compiler:
Compile command;
icpc -o run main.cpp bath_setup.cpp density.cpp propagation.cpp transition_matrix.cpp opt_parser.cpp -lgsl -lgslcblas -lm -qopenmp -std=c++11
Run command:
export OMP_NUM_THREADS=[number of OpenMP threads]; ./run Input
MPI version:
module load intel/2018u4
module load gsl/intel/2.5
module load gcc/8.2.0
Compile command;
mpic++ -o run main.cpp bath_setup.cpp density.cpp propagation.cpp transition_matrix.cpp opt_parser.cpp -lgsl -lgslcblas -lm -std=c++11
Run command:
mpirun -n [number of MPI processors] ./run Input
Errors:
A frequent error encountered while compiling is: “fatal error: gsl/gsl_rng.h: No such file or directory”
This can occur if the directory is not installed on the standard search path of the compiler. It can be fixed by adding it’s location as a flag in the compile command as exaplained in this link: Using the GSL Library.
On Kay the flags ‘-I/ichec/packages/gsl/gcc/2.5/include’ and ‘-L/ichec/packages/gsl/gcc/2.5/lib’ must be added to the compile command as:
g++ -o run main.cpp bath_setup.cpp density.cpp propagation.cpp transition_matrix.cpp opt_parser.cpp -lgsl -lgslcblas -lm -fopenmp -std=c++11 -I/ichec/packages/gsl/gcc/2.5/include -L/ichec/packages/gsl/gcc/2.5/lib
Checking for accuracy¶
The original serial code was run 1000 times to generate an expected output and variance. These can be found in the ./Regression_testing sub-directory. A regression test is built into both the OpenMP and MPI versions which checks if their output is within five standard deviations of the expected output (given a specific set of input parameters). If any part of the output goes outside that limit the regression test will fail. (Note: To run a test ‘Regression_test=1’ must be set in the Input file along with a standard set of parameters. All of this is specified in the Input file).
Testing, Performance and Scaling¶
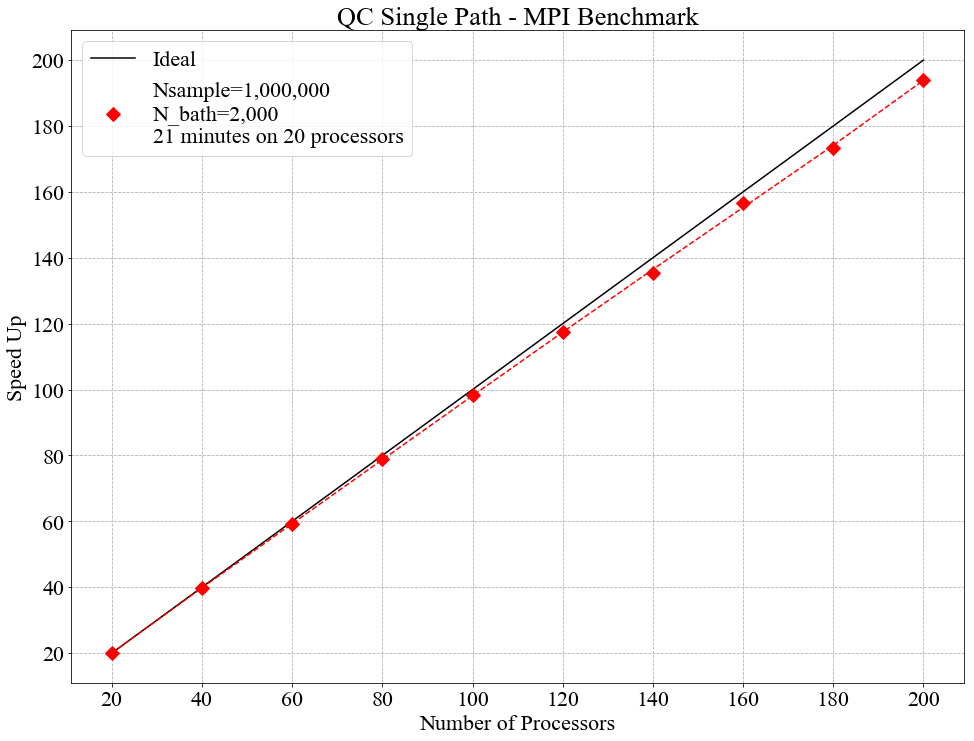
Testing was performed on the Kay supercomputer from ICHEC. Kay is separated into nodes, each of which has 2 x (20 core) sockets. To test the parallel efficiency of both the OpenMP and MPI versions of the code they were benchmarked on 20 - 200 cores (1 - 5 nodes).
The OpenMP version was run for 10,000,000 samples (Nsample = 10,000,000) and for a bath size of 200 (N_bath = 200). As can be seen in the graph below OpenMP scales perfectly on a single node (i.e. less than 40 cores), but provides little to no benefit over multiple nodes.
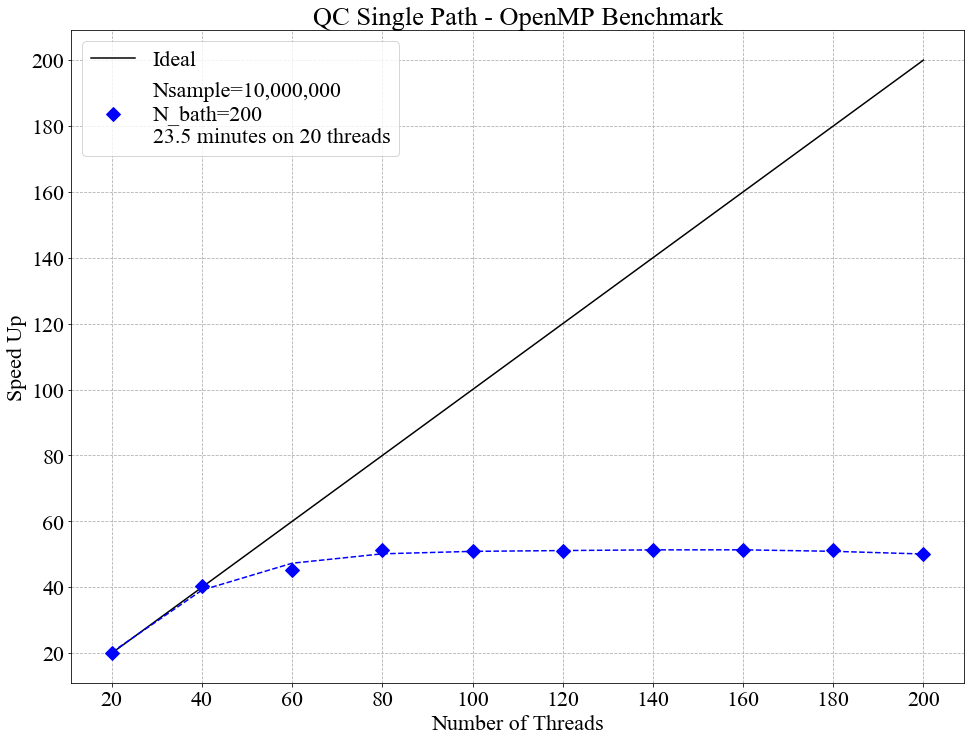
The MPI version was run for 1,000,000 samples (Nsample = 1,000,000) and for a bath size of 2,000 (N_bath = 2,000). MPI scales very well over the entire benchmark (up to 200 cores), with an average efficiency of 96.3%.
Source Code¶
The source codes for the OpenMP and MPI versions of the code are:
Source Code Documentation¶
The source code documentation is given at https://gitlab.e-cam2020.eu/Quantum-Dynamics/Surface-Hopping/tree/master/Doc.
These documentation files can be updated by executing the make command in the Doc directory.
References¶
| [Mackernan] | (1, 2) D.Mackernan, G.Ciccotti, R.Kapral, Trotter-Based Simulation of Quantum-Classical Dynamics, J. Phys. Chem. B, 2008, 112 (2), pp 424-432. |