CLstunfti¶
Purpose of Module¶
CLstunfti is an extendable Python toolbox to compute scattering of electrons with a given kinetic energy in liquids and amorphous solids. It uses a continuum trajectory model with differential ionization and scattering cross sections as input to simulate the motion of the electrons through the medium.
Originally, CLstunfti was developed to simulate two experiments: A measurement of the effective attenuation length (EAL) of photoelectrons in liquid water [01] and a measurement of the photoelectron angular distribution (PAD) of photoelectrons in liquid water [02]. These simulations were performed to determine the elastic mean free path (EMFP) and the inelastic mean free path (IMFP) of liquid water [03]. Additionally, a program based on CLstunfti is currently being developed which simulates electron scattering in liquids in the presence of laser fields. This extension of CLstunfti is used for simulation of attosecond experiments in liquid water.
The EMFP and IMFP are two central theoretical parameters of every simulation of electron scattering in liquids, but they are not directly accessible experimentally. As CLstunfti can be used to determine the EMFP and IMFP from experimental data, and as it can be easily extended to simulate other problems of particle scattering in liquids, it was decided to make the source code publicly available. For thus purpose, within the E-CAM module a documentation for the code was written and examples were designed to test the code and learn how to use CLstunfti.
| [01] | Suzuki, Nishizawa, Kurahashi, Suzuki, Effective attenuation length of an electron in liquid water between 10 and 600 eV, Phys. Rev. E 90, 010302 (2014). |
| [02] | Thürmer, Seidel, Faubel, Eberhardt, Hemminger, Bradforth, Winter, Photoelectron Angular Distributions from Liquid Water: Effects of Electron Scattering, Phys. Rev. Lett. 111, 173005 (2013). |
| [03] | Schild, Peper, Perry, Rattenbacher, Wörner, An alternative approach for the determination of mean free paths of electron scattering in liquid water based on experimental data, submitted. |
Background Information¶
Within this E-CAM module, the necessary steps were taken to make CLstunfti a useful toolbox for other researchers by providing a documentation, examples, and also extensive inline documentation of the source code. CLstunfti is available at https://gitlab.com/axelschild/CLstunfti and is published together with the E-CAM module.
Building and Testing¶
To use CLstunfti, the following steps are necessary:
- A few Python packages are needed. Specifically, you need:
- h5py==2.10.0
- matplotlib==3.2.2
- scipy==1.5.0
- numexpr==2.7.1
- numpy==1.19.0
Move the main folder
CLstunftiin a folder named e.g.My_Python_Modules. Then, either runpython setup.py build_ext --inplace
in the main folder or change to the
CLstunftisubfolder and runf2py -c --opt='-O3 -ffast-math' ftools.f95 -m ftools
to compile the Fortran code as a module. To make Python know where CLstunfti is, run
export PYTHONPATH=$PYTHONPATH:$HOME/My_Python_Modules/CLstunfti
in your shell or add the line to the end of your
.bashrc(or.zshrcor.cshrc) file.Build the documentation by running
make html
It is found in
_build/html(actually, it should already be there).Use CLstunfti!
The examples created for this E-CAM module are in the folder examples.
Each example comes with a sample output which has the same name as the files
created by the scripts, but appended with _ref.
Some of the examples have a rather long runtime, as indicated below.
This is because the examples should also show what is needed to compute the
relevant targets correctly. If a quick test is preferred, the number of
trajectories can be decreased.
The following examples are provided (note that part of the code is in the file
tools_eal_pad.py in the example folder):
Example 01 shows how to prepare an input for CLstunfti. It is run as
python 01_create_input.py
It will create the HDF5 file
prop_data.h5which can be compared with the reference fileprop_data_ref.h5.Example 02 shows how to compute the effective attenuation length (EAL), i.e., the effective/average depth from which photoelectrons are ionized. This is done by selecting many ionization depths
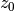 and by fitting the
number of electrons detected outside the liquid to
and by fitting the
number of electrons detected outside the liquid to
It is run as
python 02_compute_eal.py
and creates
02_eal.pdfwhich can be compared with02_eal_ref.pdf. The calculation takes ca. 1 minute on a 3.40GHz CPU.Example 03 shows how to compute the photoelectron angular distribution (PAD) of electrons that leave the liquid after photoionization. This is done by rotating the PAD for photoionization (which simulates a rotation of the laser used for ionization) away from its default direction (the
 -axis, as the default is that
-axis, as the default is that  is the liquid and
is the liquid and
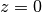 is the surface) and by detecting the number of electrons outside
the liquid depending on the polar angle
is the surface) and by detecting the number of electrons outside
the liquid depending on the polar angle 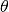 of the rotation.
The PAD has the functional form
of the rotation.
The PAD has the functional form
where
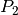 is the Legendre polynomial of second order. Hence, the PAD
is fully characterized by the parameter
is the Legendre polynomial of second order. Hence, the PAD
is fully characterized by the parameter 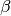 .
.Two ways to do the calculation are provided. The first uses importance sampling of the ionization depth with an exponential distribution, is run with
python 03a_compute_pad.py
and creates
03a_pad.pdfwhich can be compared with03a_pad_ref.pdf. The calculation takes ca. 1 hour on a 3.40GHz CPU.The second way uses a linear sampling, where initial positions are added until deeper and deeper in the liquid until no trajectories are leaving it anymore. It is run with
python 03b_compute_pad.py
and creates
03b_pad.pdfwhich can be compared with03b_pad_ref.pdf. The calculation takes a few hours on a 3.40GHz CPU.Example 04 shows how to find elastic and inelastic mean free paths if an EAL and PAD are given. From an initial guess for the EMFP and IMFP, it optimizes their values by comparing the calculated EAL and PAD with a target EAL and PAD. It is run with
python 04_find_emfp_imfp.py
and provides the terminal output given in
04_find_emfp_imfp_output.txtfor comparison. The calculation takes ca. 1 hour on a 3.40GHz CPU.Example 05 compares the angular distribution of photoelectrons after ionization, one scattering, two scatterings, etc. in the bulk (no surface) with the known solution. There are four parts. The calculations should be performed in the right order because the results are saved to files.
In the first part, the angular distribution of the electrons after up to nine scatterings in the bulk without inelastic scattering is computed. It is run with
python 05a_bulk_prep.py
and creates
05a_bulk.pdfand05a_bulk.h5which can be compared with05a_bulk_ref.pdfand05a_bulk_ref.h5, respectively. The calculation takes ca. 1.5 hours on a 3.40GHz CPU.In the second part, results of the first part are compared with a convolution of the initial PAD with the DSCS and with doing the exact equivalent of the convolution (the convolution only gives the exact result in 2D, in 3D it is more complicated). It is run with
python 05b_compare_bulk_convolution.py
and creates
05b_compare_bulk_convolution.pdfwhich can be compared with05b_compare_bulk_convolution_ref.pdf. The calculation takes a few seconds on a 3.40GHz CPU.In the third part, the angular distribution of the electrons after up to nine scatterings is computed outside the surface. It is run with
python 05c_surface.py
and creates
05c_surface.pdfwhich can be compared with05c_surface_ref.pdf. The calculation takes ca. 10 minutes on a 3.40GHz CPU.In the fourth part, the results of the first and third part are compared. It is run with
python 05d_comparison_bulk_surface.py
and creates
05d_comparison_bulk_surface.pdfwhich can be compared with05d_comparison_bulk_surface_ref.pdf. The calculation takes a few seconds on a 3.40GHz CPU.
Source Code¶
For the module, the documentation and the examples were developed and the source code of CLstunfti was extensively commented.