LocConQubit¶

Purpose of Module
Local Control Theory (LCT)
Applications of the Module
Installation
Testing
Source Code
Source Code Documentation
References

Purpose of Module ¶

LocConQubit is a code for constructing controlled pulses on isolated qubit systems that can either drive the population between specific qubit states or work as a logical gates between qubits. LocConQubit implements the Local Control Theory (LCT) which generates the required pulses on-the-fly. The generated pulses can be further post-processed with a variety of tools accompanying the LocConQubit module in order to obtain an optimal control pulse.

Local Control Theory (LCT)¶

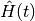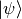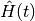In general Local Control Theory is an on-the-fly procedure for updating the time-dependent Hamiltonian ( $\hat{H}(t)$ ) to achieve population transfer from some initial quantum state to a designated quantum target state ( $| \psi \rangle$ ). 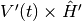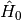[LCT1] [LCT2] LCT achieves its full capacity if the time-dependent component of the full system Hamiltonian $\hat{H}(t)$ can be decomposed as an external perturbation ( $V^{\prime}(t) \times \hat{H}^{\prime}$ ) acting on a system with a time-independent Hamiltonian ( $\hat{H}_{0}$ ),

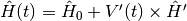$\hat{H}(t) = \hat{H}_{0} + V^{\prime}(t) \times \hat{H}^{\prime}$ ,

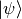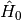and if the targeted quantum state $| \psi \rangle$ is an eigenstate of the same time-independent Hamiltonian $\hat{H}_{0}$ ,

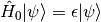$\hat{H}_{0} | \psi \rangle = \epsilon | \psi \rangle$ .

LCT in this case constructs a time-dependent perturbation 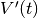$V^{\prime}(t)$ from the expression

$V^{\prime}(t) = -i \langle \Psi(t) | \Big[ \hat{H}^{\prime},| \psi \rangle \langle \psi | \Big] | \Psi(t) \rangle$ ,

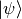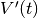which will achieve the required population transfer from any initial state to the $| \psi \rangle$ target state. The new time-dependent potential component $V^{\prime}(t)$ updates the time-dependent component of the full Hamiltonian describing the evolution of the system via the time-dependent Schrödinger equation

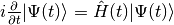$i \frac{\partial}{\partial t} |\Psi(t)\rangle = \hat{H}(t) |\Psi(t) \rangle$ .

The LCT procedure is applied sequentially in small integration steps $[t,t+\delta t]$ within the propagation of above equation until the population has been completely transferred to the designated target state. The schematic below illustrates the LCT procedure.

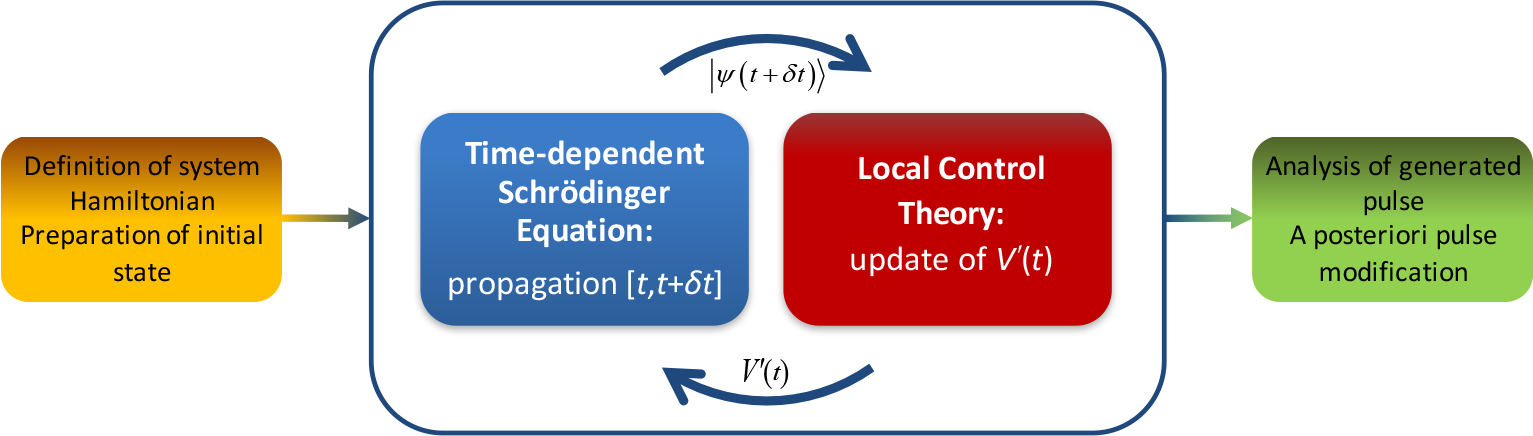
Applications of the Module ¶

Application of the LCT module can be found at the pilot project web page.

Installation ¶

The LocConQubit is a Python based code. The module requires the presence of QuTip (version 4.1 or above) program package and the modules accompanying QuTip (namely: numpy (version 1.13 or above), scipy (version 0.18 or above), matplotlib (version 2.10 or above)). A Python interpreter 3.5 or above is required, because the module has not been used with Python 2 versions. Instructions on how to install the QuTip and the accompanying program packages can be found on this link. Upon the successful installation of QuTip, all other required packages will be present. It is highly recommended to verify the QuTip after its installation. Instructions for QuTip testing are provided on the installation page.

Testing ¶

Proper functionality of LocConQubit module can be verified by performing the unit tests simply by executing the below command in the directory containing all LocConQubit module files

python test_LCT.py

where python is an alias for a Python 3.5 version interpreter or higher. Five unit tests are executed sequentially and all must pass successfully in order to use the LocConQubit module.

Source Code ¶

The LocConQubit module source code is located at: https://gitlab.e-cam2020.eu:10443/Quantum-Dynamics/QC.

Source Code Documentation ¶

The source code is accompanied with sphinx documentation located in sub-directory ./doc. Instructions for sphinx installation can be found here. The html documentation files can be obtained by executing the following command in the ./doc sub-directory

cd ./doc

make html

The generated documentation is located in the ./doc/_build/html/index.html.

References ¶

[LCT1]

B. F. E. Curchod, T. J. Penfold, U. Rothlisberger, I. Tavernelli Phys. Rev. A 84 (2012) 042507 DOI: 10.1103/PhysRevA.84.042507

[LCT2]

B. F. E. Curchod, T. J. Penfold, U. Rothlisberger, I. Tavernelli Chem. Phys. Chem. 16 (2015) 2127 DOI: 10.1002/cphc.201500190